SCS-100T U 型汽车衡秤体结构优化

针对目前汽车衡秤体结构材料利用率低、质量大的问题，将结构优化设计的方法引入到秤体结构设计中。以 U 型梁和秤台的几何尺寸为设计变量，秤体的最大挠度为约束条件，秤体整体质量为目标函数，利用参数化 APDL 语言建立了秤体结构的有限元优化模型，对秤体结构进行了优化分析，从而确定了 U 型梁和秤台的几何尺寸。研究结果表明，在满足秤体刚度和强度设计要求的前提下，秤体结构优化后的质量比原来的降低了 6． 7% ，实现了降低秤体结构质量的目的，提高了材料利用率。

0.引言

随着汽车衡器不断的发展，其秤体结构也不断地推陈出新。在经历了几代变革之后，U 型汽车衡已经成为市场的主流产品。然而，国内很多企业在进行秤体结构设计的过程中仍处于简单模仿国外产品，凭借经验设计或是简单的理论计算，导致秤体结构的设计过于安全，刚度过大，结构偏重，材料利用率不高，制造成本偏高。

近年来有一部分科研工作者在 U 型梁秤体结构设计方面做了一些研究。将秤体简化为一简支梁，从理论上对 U 型梁的秤体结构进行了受力通过对不同秤体结构方案进行理论计算及比较分析，认为 U 型结构的秤体具有性能好、重量轻的特点; Taowei Shi 等利用有限元法对SCS 系列 120 t 汽车衡秤体结构中单个秤体在不同加载方式下的变形情况进行了研究。

本研究利用有限元及优化理论，以某公司生产的SCS-100T U 型梁汽车衡秤体结构为原型，采用有限元结构分析软件，建立整体秤体结构有限元模型进行优化分析，在满足设计要求的前提下实现秤体结构的轻量化，对汽车衡秤体结构的设计生产具有参考价值。

1.秤体结构

SCS-100T U 型梁汽车衡秤体结构的原始参数来自某公司生产的汽车衡，该汽车衡由 3 个秤体组成，整体结构尺寸为 16m(长） × 3 m ( 宽 )  × 0． 362 m( 高) ，最大秤量重量为 100 t，秤量方式为静态整车秤量。

3 个秤体 U 型梁的分布情况均相同，如图 1( b) 所示。每个秤体都有 6 根 U 型梁，左右对秤分布，整个秤体由 8 个传感器支撑，3 个秤体之间通过连接销搭接在一起，3 个秤体之间互相作用，为了使研究的问题更符合实际，本研究以整个秤体为研究对象。秤体与更符合实际，本研究以整个秤体为研究对象。秤体与秤体之间还有一些盖板，吊装件以及装饰件，因对研究问题影响很小，笔者去掉这些零部件，简化之后秤体的结构示意图如图 1 所示。

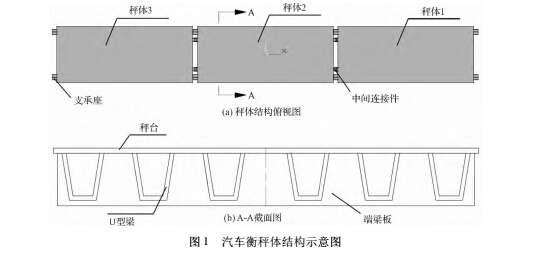
2.  秤体结构优化

2． 1  秤体结构有限元模型

整个秤体结构材料均采用 Q235 钢，其屈服极限为 235 MPa，弹性模量为 206 GPa，泊松比为 0． 3，密度为 7 850 kg / m3 。根据汽车衡秤体结构原始数据，本研究利用参数化 APDL语言建立其有限元模型。在划分网格时，考虑到秤台和 U 型梁厚度尺寸远远小于其纵向尺寸，如果采用实体单元，则需要画得非常细，网格数量就会增加很多，造成计算资源浪费，而采用壳单元既可满足分析问题的要求，又能减少计算量，故本研究采用壳单元 SHELL63对秤台和 U 型梁进行网格划分，秤体的其余部分均采用实体单元 SOLID185 进行网格划分。U 型梁、支承座与端梁板的连接处采用MPC 接触算法对节点进行耦合。

汽车衡器的秤体结构设计以刚度作为主要的校核指标，一般秤体刚度在满足设计要求的情况下强度也能满足要求，根据 GB / T 7723-2008《固定式电子汽车衡》关于大型衡器的承载器最大相对变形量的规定，对于最大秤量为 100 t 的衡器，须用 40 t 的载荷在承载器中间 2． 6 m 宽的区域加载检测，衡器承载器的最大相对变形在新安装后的首次检定必须小于 L /800   ，则每个秤体的挠度不能超过 D = ( 1 /3) × ( L /800) = 6． 67 ×10 － 3 m。秤体检测的加载方式如图 2( 阴影区域) 所示。

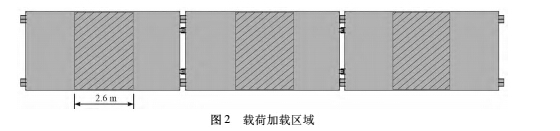
本研究选取每个秤体秤台中间 3 m × 2． 6 m 区域内的单元，将 40 t 的砝码载荷转化成压力加载到选取的单元面上，即 p = 40 × 104 / ( 3 000 × 2 600) ≈0． 051 3。考虑到支承秤体德传感器固定在地面上，而秤体在承受载荷变形时支承座与传感器之间存在相对运动，故取 8个支承座与传感器间的接触处中的一处施加 UX 、UY 、UZ3 个方向的约束，其余 7 处只施加 UZ 方向的约束。

2． 2  秤体结构优化设计的数学模型

在优化设计时太多的设计变量会使得计算收敛于局部最小值的可能性增大，同时越多的设计变量需要越多的迭代次数，从而需要更多的机时。为了尽量使用较少的设计变量，本研究首先按照表 1 中两种不同 U 型梁布置方案改变的秤体结构模型参数，进行有限元分析，两个方案秤体结构的最大挠度和秤体重量如表 1 所示。

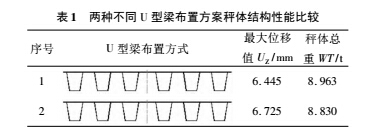
从表 1 中可以看出，虽然方案 2 秤体结构的刚度和质量比方案 1 的有所下降，但是下降得不多。考虑到实际工况下大吨位的载重车的轮间距较大，因此本研究选择方案 1 作为下面进一步优化的结构模型，即3 个秤体的 U 型梁全部按照一种尺寸大小进行布置，梁与梁之间的水平距离保持不变。

秤台和 U 型梁作为汽车衡秤体结构的主要组成部分，汽车衡的重量主要集中在这两部分上，因此在保持秤体结构本身的形状不变的情况下，改变上盖板和U 型梁的尺寸，即以上盖板厚度 T1 、U 型梁开口角度θ、高度 H、底部宽度 B 及其厚度 T2 为设计变量，秤体最大挠度 DISP≤6． 6 mm 为约束条件，秤体结构总重量 WT 为目标函数，在满足秤体结构刚度要求的情况下使秤体结构总重量最轻。秤体结构优化的数学模型表述为:

min  WT( x) ，x ＞ 0                （1）

s． t g( x) = DISP － 6． 6≤0，x ＞ 0     （2）

式中: WT( x) —目标函数; x—设计变量，x = ( θ，T1 ，T2 ，H，B) ; g( x) —约束函数。

3.秤体结构优化结果分析

3． 1  优化计算结果

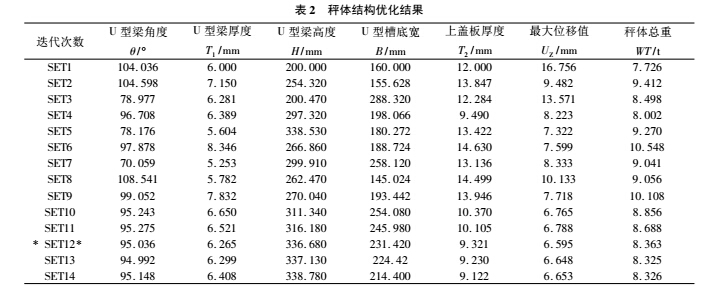
通过分析计算，优化结果如表 2 所示。从表 2 中可以看出，* SET12* 是最佳优化系列。其优化结果为U 型梁角度 θ = 95． 036°，U 型梁厚度 T1 = 6． 265 mm，U型梁高度 H = 336． 680 mm，U 型梁槽底宽 B = 231． 420 mm，上盖板厚度 T2 = 9． 321 mm，秤体的最大位移 UZ = 6． 595 mm ＜ 6． 6 mm，符合设计要求，这时的秤体结构总重量 WT = 8． 363 t。

3． 2 优化方案与初始方案比较分析

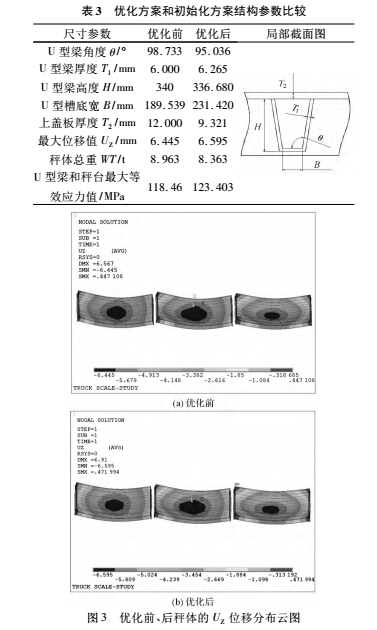
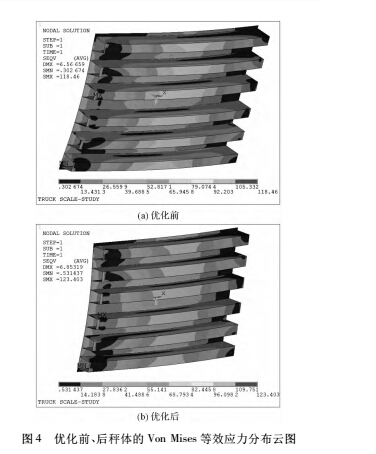
优化前、后秤体结构参数比较如表 3 所示。从表3 中可以看出，优化后新秤体结构的总重比原秤体结构降低 6． 7% ，材料用量的减少主要来自上盖板厚度的减少。本研究对优化的方案进行有限元分析，以验证新的秤体结构的刚度和强度是否符合设计要求，优化前后的秤体结构位移 UZ 分布云图如图 3 所示。从图 3 中可以看出最大位移 UZ 均发生在秤体中部，优化后的最大位移 UZ 值增加了 0． 15 mm，但小于设计允许的最大值 6． 6 mm，满足刚度要求。优化前后秤体的Von Mises 等效应力分布云图如图 4 所示。从图 4 中可知，优化前、后秤体的秤台和 U 型梁的最大 Von Mises等效应力均发生在第 2 个秤体的 U 型梁左端与端梁板的连接处，分别为 118． 46 MPa 和 123． 403 MPa，优化后较优化前有所增大，但都小于材料的屈服强度，满足强度要求。

4.结束语

本研究以某公司生产的汽车衡秤体结构为基础，利用参数化 APDL 语言建立了秤体结构的有限元优化模型。以汽车衡秤体结构质量最小为目标，刚度为约束条件，U 型梁的厚度、开口角度、高度以及秤台的厚度为设计变量，对秤体结构进行了优化分析，优化结果给出的汽车衡秤体结构，材料利用率提高，轻量化效果显著。并与原秤体结构进行性能对比分析，研究结果表明，优化的结果是可行的。