电子秤测量不确定度的概念简析及应用实例

测量不确定度的评定与表示是计量工作中的重要一环，在计量实验室认证、授权考核等工作中， 都需要用到这方面的知识。 由于不确定度的概念描述十分晦涩难懂，评定过程、数据分析又很繁琐， 导致很多刚刚接触这个概念的计量工作人员感到十分困惑。 鉴于许多初学者不能很好的区分测量不确定度和测量误差这两个概念， 所以我们需要先对它们做一个区分说明。 测量误差是指用测得的量值减去参考量值所得出的值， 其目的是表明测量结果偏离参考量值 （在不是十分严谨的情况下也可以简单理解为真值）的程度。举例来说，一台最大秤量为220g，准确度等级为一级的电子天平， 用 F1级标准砝码进行检定， 在200g称量点上的测量误差为 0.5mg， 表达的含义是这一次的检定结果与参考值的差为 0.5mg， 如果重复操作， 误差值可能会不同。而测量不确定度是指根据所用到的信息， 表征赋予被测量值分散性的非负参数， 其目的是表明被测量值的分散性，其来源是由于测量的不完善和人们认识的不足，使被测量值每次测得的结果不是同一值， 而是以一定的概率分散在某个区域内的许多个值。 在同条件下举例， 经计算得出， 在200g的称量点上，

这台电子天平的扩展不确定度 U=0.84mg （k=2），表达的含义是在200g的称量点上， 合成了各个不确定度分量之后， 这台天平的被测量值有95%的概率分布在[200±（0.84×10-3）]g的区间内。用扩展不确定度来表示是因为标准偏差 u 的包含区间只有68%， 从统计学的角度来看， 这个概率太低了，所以一般取置信因子 k=2， 把包含概率提高到95%。从上文可以很明显的看出，两者在测量的目的和表达的含义上， 有着本质的区别。 简单分析后， 我们以电子天平的不确定度评定为例， 进行不确定度的计算并进一步阐述一些相关概念。

我单位计量实验室配有电子天平一台， 准确度等级为一级，最大秤量为220g，分度值 d=0. 1mg，实验室另配置有 F1级200g标准砝码1个，该砝码处于检定有效期内， 实验室温度为20℃，温度波动不大于 0.5℃/h， 相对湿度60%。请在200g称量点上对该天平的测量结果进行不确定度的评定。

由上面给出的条件我们知道，  电子天平测量结果的不确定度是由 4 个不确定度分量合成的，分别是被检天平测量重复性导致的不确定度分量u1，标准砝码误差导致的不确定度分量u2， 电子天平分辨力导致的不确定度分量 u3，以及温度不稳定和振动因素导致的不确定度分量 u4。

（1） 测量重复性导致的不确定度分量 u1，这需要我们采用 A 类评定方法，即对测得的量值用统计分析的方法进行测量不确定度分量的评定。测量的次数不宜太少，否则会影响标准偏差的可靠程度，所以我们选择做 10 次重复性测量，结果分别为：

200.0008g，200.0004g，199.9999g，199.9996g，200.0004g， 200.0006g， 200.0008g， 200.0002g， 200.0003g，200.0006g。

我们可以得出观测列的平均值 =200.00036g

根据贝塞尔公式：

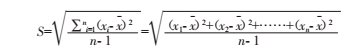
（2） 标准砝码误差导致的不确定度分量 u2，我们采用 B 类评定法。

根据 JJG 99- 2006 《砝码检定规程》 我们知道质量为 200g 的 F1 级标准砝码最大允许误差的绝对值为 1mg，折算质量的扩展不确定度 U（k=2），应不大于其最大允许误差绝对值的三分之一，我们取最大值，即等于三分之一最大允许误差的值，U=（1mg）/3。

因此 u2=U/2=（1mg）（/2×3）=0.17mg。

（3） 电子天平分辨力导致的不确定度分量 u3，我们同样采用 B 类评定法。根据 JJF 1059.1- 2012《测量不确定度评定与表示》 的相关内容我们知道，数字显示器的分辨力导致的不确定度，通常假设可能值在区间内为均匀分布，均匀分布的置信因子 k 值为根号 3 （以下写作 1.732），不确定度分量为 a/1.732。电子天平的分度值 d=0.1mg，由以上信息我们可以得出：

u3=a/k=δx/ （2×1.732）=0.03mg （δx 为显示器的分辨力，a 为区间半宽度）

（4） 由温度不稳定和振动因素导致的不确定度分量 u4。在实验室条件下，由环境温度的变化和周围振动引发的不确定度分量予以忽略，不代入后续计算。

综合以上信息，我们已经得到了影响合成标准不确定度的四个分量，而且，这四个不确定度分量之间并不相关，即不存在相互间的函数关系，所以合成标准不确定度采用公式：

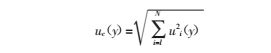
所以该天平在 200g 的称量点上，其扩展不确定度 U=0.84mg（k=2）

至此，该电子天平在 200g 的称量点上，其测量不确定度的评定已经完成。最后，有一些问题还需要我们重视：（1）对衡器的测量结果进行不确定度的评定，必须使用上一级的标准砝码。举例来说，如果你使用 M1 级砝码对一级电子天平进行不确定度的评定，是不符合规程的，因为该天平可对 M1 级砝码的质量进行标准不确定度的评定，反过来则是不可以的。（2）A 类评定中有两种较为常用的计算方法，分别是文中使用的贝塞尔公式法和极差法，极差法计算简单，但是可靠性相对较低，在测量次数 n<10 情况下比较适用，如果使用贝塞尔公式法，则 n 值应尽量大于等于 10，因为 n 值越大，贝塞尔公式法的可靠性越高。（3）关于 B 类评定法，是基于其他方法估计概率分布或者分布假设来评定标准差并得到标准不确定度的，它只能得出这一类标准器或装置的不确定度属性而无法反映个体间不确定度的差异。