基于遗传算法 SVM 的地磅智能称重系统研究
文章主要针对传统的模拟称重系统存在各类误差补偿困难的问题,提出了一种基于遗传算法 SVM 的非线性补偿数学模型,实现误差补偿,从而提高了整个称重系统的检定分度值。
0.引言
随着经济的高速发展和工作效率的提高,地磅称重系统在性能方面朝着高准确度、高速度、高稳定性、多功能多接口等方向发展,在结构方面朝着组合化、模块化等方向发展。因此,高准确度远程数字称重系统无论是在服务社会经济发展,还是在提高我国地磅企业的技术水平都有着一定的重要意义。
针对传统的模拟称重系统存在各类误差补偿困难,角差调整过程繁琐,稳定性和可靠性低以及难以实现在线监测等诸多问题,本文提出了一种基于遗传算法 SVM 的地磅智能称重系统,结合人工智能数据处理技术,在称重系统中建立起基于遗传算法 SVM 的非线性补偿数学模型,用于实现误差补偿,使得整个称重系统的检定分度数得到提高。
1.基于遗传 SVM 的非线性补偿
近几年来称重传感器校正模型被广泛使用的人工神经网络 ( Artificial Neural Network,ANN) ,非线性逼近能力方面具有非常明显的优势,常见的有 BP 神经网络、RBF 神经网络、广义回归神经网络方法等。人工神经网络 ( ANN) 同样存在一定缺陷,如训练速度较慢,存在过拟合现象,易产生局部最小点以及泛化能力比较弱等问题,所以这种类型的补偿方式也很难实现预期的高精度。
支持向量机 ( Support Vector Machine,SVM)是一种新的机器学习方法,建立在统计学习理论( Statistical Learning Theory,SLT) 的基础上,其工作原则是以结构风险最小化为核心,通过提高泛化能力来确保结果为可得的最优解,这也较好地解决了非线性、小样本等问题。但是,运用这种算法时,如何有效选择核函数、确定参数等问题仍然存在争议。
目前,传感器非线性校正领域中已经大批量使用支持向量机 ( SVM) 技术,但是其惩罚系数C、损失函数参数 ε 以及核函数参数的选取问题还没有找到一种合适的方法来解决。本文中将结合遗传算法来将上述问题最小化。遗传算法是一种随机优化算法,这种算法不是单纯随机比较搜索,而是靠对染色体的评价和对其中基因的作用,依靠已有的信息来指导搜索并对质量的状态进行改善。遗传算法对需要求解的问题,没有连续性、可微性方面的要求,只需要知道目标函数的相关信息即可。因此,本文认为遗传算法是解决上述问题的一种简单可行的最优方法。
本文中将遗传 SVM 方法引入校正模型中,利用遗传算法的强大全局搜索能力,构建了一种更加完善的称重传感器输出特性校正模型。
1. 1 基本原理
称重传感器的输出特性为: y = f( x,t1 ,t2 ,…,tn ) ( 1)
式中: x 为传感器的输入量; t1 ,t2 ,…,tn 为 n 个非目标参量; y 为称重传感器输出。
利用遗传 SVM 进行称重传感器的输出特性的校正原理如图 1 所示。
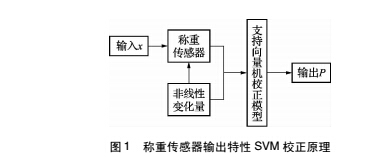
若 t、y 为 x 的单值函数,则式 ( 1) 存在反函数,即 x = f - 1 ( y,t1 ,t2 ,…,tn ) ,这个反函数是一个很复杂的数学模型,用具体的函数来表达存在一
定困难,因此可利用支持向量机校正模型来尽量表现出这种非线性关系。将称重传感器的最终输出结果值 y 和非目标参量 t1 ,t2 ,…,tn 等数据,当作支持向量机校正模型的输入值,在其运算后输出结果为 P,那么 P 则为去除了非目标参量等影响后的目标参量。
1. 2 SVM 校正模型
在称重传感器中运用 SVM 进行输出特性的校正,根本上就是考虑回归问题。参与这类回归问题分析的样本只有一种类型,即可以达到使所有样本离最优分类面的偏差最小的最优分类面。
SVM 校正模型的工作原理是: 运用非线性映射 ,在获取输入数据后将其反应到高维空间,并在高维空间转换后进行回归分析,构建输入值y、t1 ,t2 ,…,tn 与输出值 P 的函数关系。换言之,这类校正模型可用 SVM 回归分析问题来解释,即假设称重传感器所获取的输入值和输出值所构成的数据样本集表示为 { xi ,yi } ,i = 1,2,…,n,其中,xi 为称重传感器的输入且 xi ∈RN ,yi为称重传感器的输出且 yi ∈RN ,那么 SVM 校正模型所需要研究的问题可以表述为如下的回归函数形式:

式中: ω· ( x) 为向量 ω 与 ( x) 的内积; ω 的
维数为高维空间维数; b 为阈值且 b∈R。
实际应用中,为了求解 ω 与 b,一般引入松弛变量 ξ( ξ* ≥0) ,则最优化问题就转变为求下式最优解:

1. 3 基于遗传 SVM 的传感器非线性校正模型
下文将以径向基核函数为例,简单对遗传算
法如何优化支持向量机和它的参数进行描述。实
现过程如图 2 所示。
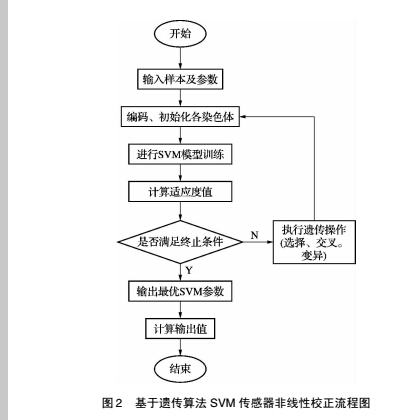
( 1) 初始化种群代数。
( 2) 确定支持向量机的惩罚系数 C、损失函数
参数 ε 和核函数参数 σ 的取值范围,组成初始种群,并以实数形式编码成染色体。
( 3) 用训练样本对每组参数进行训练,计算各个个体的适应度函数值。适应度函数值是输出值与期望值的平均相对误差。
( 4) 对种群进行选择、交叉、变异运算。
( 5) 判断是否满足终止条件 ( 本文以是否完成最大遗传代数为准则) ,若满足则输出支持向量机最优参数,若不满足则返回 ( 3) 。
( 6) 选择末代种群中最好的个体进行解码,则得到最优的 SVM 的惩罚系数 C、损失函数参数ε 和核函数参数 σ 并进行训练。
( 7) 用得到的最优的 SVM 参数计算输出值
2.实验验证
使用一只 C3 等级最大秤量为 100 kg 的称重传感器制作一秤台,连接本系统,测得如表 1 所示的数据,其中所加载荷为 F2等级砝码,显示分度值设为 1 g。
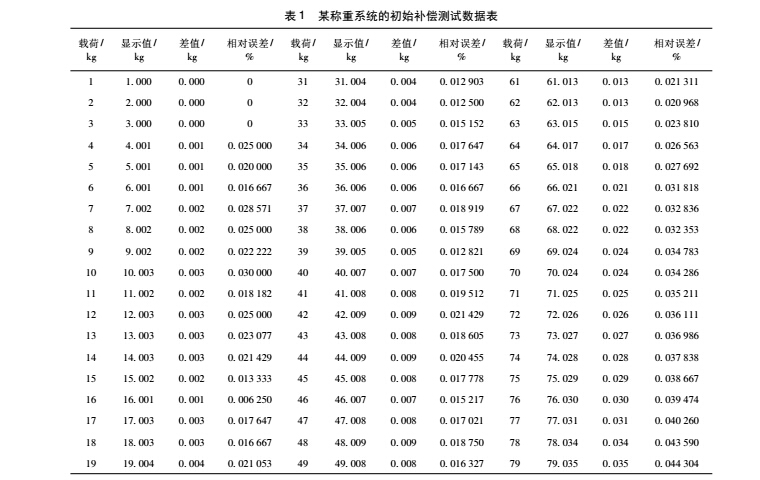
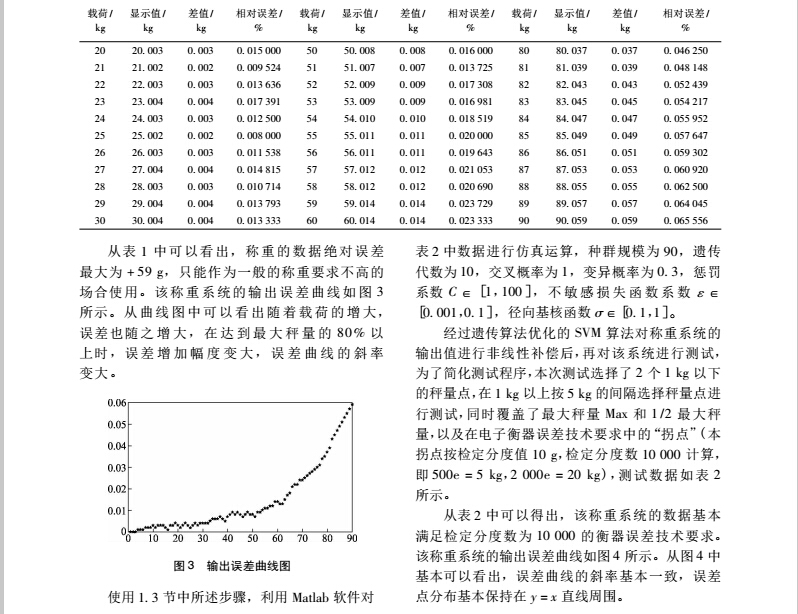
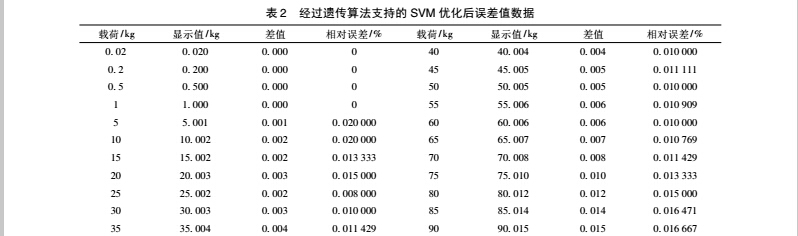
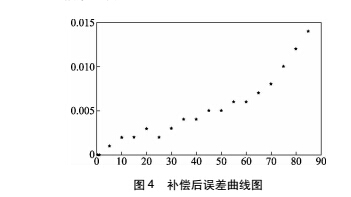
从补偿后的数据来看,该称重系统的性能基本能达到分度数为 10 000 的三级衡器要求,相比之前的性能有了一定程度的提高。
3.结束语
本文主要是结合人工智能数据处理技术,在称重系统中建立起基于遗传算法 SVM 的非线性补偿数学模型,实现误差补偿,提高整个称重系统的检定分度数值,根据实验结果可知称重系统的性能基本能达到分度数为 10 000 的三级衡器要求。

